学生コンシェルジュの活動記録

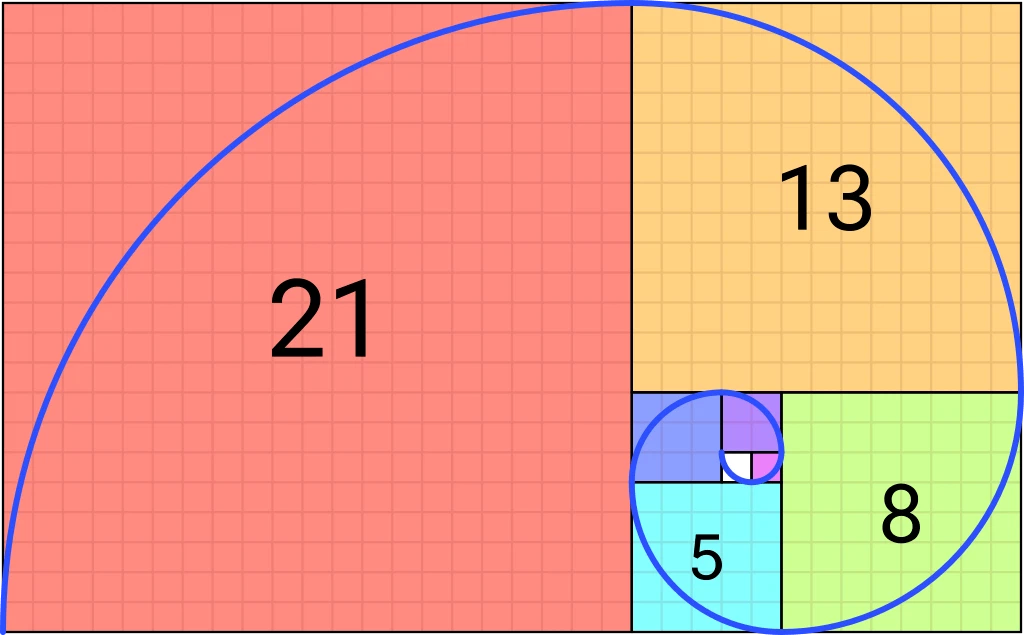
富山の夏は蒸し暑い こんにちは！金曜日13:30～15:00の学生コンシェルジュを担当しております。 理工学研究科数理情報学プログラム１年数学専攻のGENです。 夏の暑さも本格的になってきましたね。富山の場合は日本海側という事もあって湿度がほんとに高いです。加えて富山の夏は雨ばかりで晴れてることも少ないのでホントに外に出るのが億劫になりますよね。さて、今回は夏の天気に無理やり数学を関連させて台風にまつわるあの有名な数についてお話します。今回は比較的有名かつ簡単な話題なので特に知っている人もいるのではないでしょうか？教育実習などの研究授業のネタなどにしてみてはいかがでしょうか？ 大学院生GENの数学小話　第２回-フィボナッチ数列 フィボナッチ数列って何？ 今年の夏は日本に何回上陸するのでしょうか？ 気象庁の統計 によると、日本に上陸した台風の個数には年によってかなりばらつきがあるようです。今回は台風の巻いている渦に関する神秘的な数学の話をしていきます。この台風の渦の形は対数螺旋と呼ばれるもので、フィボナッチ数列というある数の並びに関連しています。フィボナッチ数列とは次のような数の並びです。 ０　１　１　２　３　５　８　１３　２１　・・・　　 簡単に説明するとこの数は左の数と自分の数の合計が右の数になる法則で続いていきます。 例　０＋１＝１、５＋８＝１３ この数列はうさぎのつがいの組数が増える様子から数学者レオナルド＝フィボナッチがみつけたと言われています。親ウサギのつがいは一か月後に子ウサギのつがいを生み、子ウサギのつがいは一か月後に親ウサギになるという法則にし従うと先ほどの数が現れます。 　　　　　最初　　１月　　２月　　　３月　　　４月　　　５月  親ウサギ     １     　　１　　　２　　　　３　　　　５　　　　８ 子ウサギ     ０     　　１　　　１　　　　２　　　　３　　　　５ フィボナッチ数列と対数螺旋 ここまでは台風の螺旋が関連しているフィボナッチ数列について説明しました。ここで、一辺がフィボナッチ数列の正方形を配置させて次のように長方形を拡大させていくことを考えます。するとつぎのような螺旋が見えてきます。 　　　　　 世界におけるフィボナッチ数列と関連...

暑さが苦手なGENからの挨拶 こんにちは！金曜日13:30～15:00の学生コンシェルジュを担当しております。 理工学研究科数理情報学プログラム２年数学専攻のGENです。 気温が本格的に高くなり、みなさんもそろそろクーラーをつけ始めたころではないでしょうか？（私は我慢できずもうとっくにつけた！電気代( ﾉД`)ｼｸｼｸ…） 水分摂取をこまめに行い、熱中症には十分気を付けていきましょう。 新シリーズ始めるか？　（ネタ切れしないかな＞＜） さて今回は私の専門分野である数学についてのお話をしていこうと思います。今後も「大学院生GENの数学小話」として、数学に関する内容をわかりやすく紹介していきたいと思います。第何回まで続くか分かりませんが、数学ってこんなところにつかわれているのかと知るきっかけになればいいと思っています。このシリーズではタイトルや文章の序盤に専門用語を用いたりする場合があります。ですが、その言葉がわからなくても楽しめる記事を意識して作成します。最初はナニソノコトバ？オイシイノ？みたいな感じで大丈夫です。記事を読み終えた後にその数学の話題がおいしいマカロンにでも見えてきたらうれしいです将来数学の教員を目指す方にも何か数学の授業のネタに使っていただけたら幸いです。数学科の学生や数学が得意な方にとっては簡単な内容かもしれません。最後に関連キーワード等を載せておきますので、その分野を学習する道しるべになればいいかなと思います。 大学院生GENの数学小話　第１回-連立一次方程式 それではGENによる数学小話第一回を始めていこうと思います。記念すべき初回の内容は「連立一次方程式」です。なにそれおいしいの？名前が長ったらしくて難しいと思うかもしれませんが、実はこの内容小学三年生の頃に扱う内容です。普段数学等を使っている人からすると簡単すぎる内容かもしれません。 連立方程式って何？ この「連立一次方程式」は次のような鶴と亀の足の本数の簡単な問題から鶴亀算とも呼ばれたりします。 鶴と亀が合わせて５匹います。足の合計は14本です。鶴と亀はそれぞれ何匹いるか？　 このような問題は鶴をｘ匹、亀をｙ匹として次のような式を立てて、いくつかの式変形をしながら解くのでした。 $\begin{equation} \left\{ \, \begin{aligned}...