ちょっと見方が変わるかもしれない確率のお話

皆さん初めまして！

今年度から学修相談スタッフになった理工学教育部１年数学専攻の森ですm(__)m 

 早速、専門分野のお話でも書こうかなと思いましたが、どうせならよりよく数学の話題を楽しめるようなことでも書こうと思います！

 皆さんに早速問題です ！

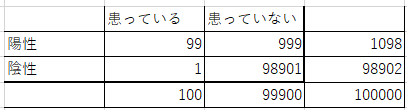
総人口の0.1%が罹患しているある病気があります。この病気の疾患の有無に使われる検査での検査精度は99%であるとき、ある人が陽性と判定されました。では、この人が本当に陽性である確率はいくつか？

 この問題をきいて、「陽性でも99%の確率で正しいのではないか？」と思った方もいらっしゃると思いますが、実際どうでしょう？

これが実際の人数に当てはめてみるとわかりやすいので、実際に100000人いるとして当てはめると、

という風になります。

ここで実際に陽性と判定された人数は1098人に当たるわけですが、実際に患ってる人数は99人

となると確率は

99÷1098=0.0901...

約9％になります。

陽性って判定されてるのに実際に患っている確率は低いですよね。この99%が実は精度が低いということがわかります。実際にそういった誤診を含んでいることも考えると、再検査を行ってより正しい判定を出すことが重要になっていきます。

もし、テレビとかの宣伝で怪しい確率を見つけたら疑ってみると面白いです(^^)